Prvky grafu

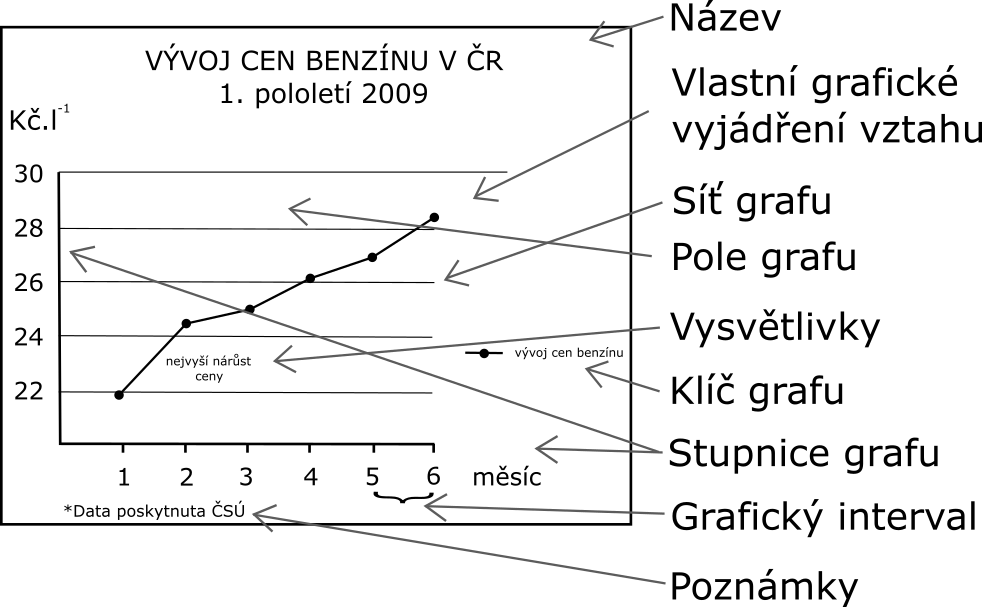
Název grafu

• Sděluje jasně a stručně obsah grafu_[1]
• Obsahuje věcné, prostorové a časové určení_[1]
  • bez uvádění zkratek_[2]
• Lze jej rozdělit na titul a podtitul_[1]
• Umístění trojím způsobem_[1]
  • na střed sítě grafu
  • do pole grafu
  • pod graf

Stupnice grafu

• = dělená linie, jednotlivým bodům je přiřazen číselný význam_[1]
• Skládá se ze základny (přímky, kružnice), kótování (body na základně) a popisu kót_[1]
  • kótováním se volí stupnice
    • rovnoměrná (aritmetická)
    • nerovnoměrná (např. logaritmická, pravděpodobnostní, empirická)_[2]
  • v jednom grafu lze použít dvě i více stupnic_[1]
• Musí mít potřebnou délku, míru přesnosti (danou modulem) a zachytit určité rozpětí hodnot_[1]
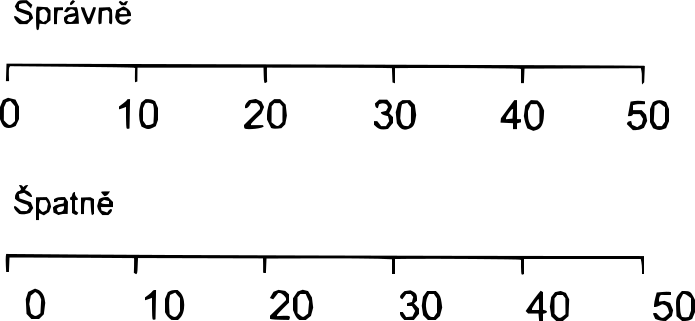
• Zásady stupnic_[1]
  • nesmí být příliš husté kótování
    • vzdálenost vyznačených bodů nemá být kratší než 5 mm
  • okótovány jsou jen ty body, které odpovídají násobkům zvoleného základu
    • při stupnici roků nesmí být letopočty ve zkráceném formátu “99, 00, 01…” ale v úplném “1999, 2000, 2001…”_[2]
  • kóty jsou umisťovány k příslušným bodům, nikoliv mimo ně
    • pouze pokud se číslem charakterizuje interval, napíše se číslo do středu úsečky
• Musí být uvedeno v jakých jednotkách je stupnice vytvořena_[2]
  • km, tuny, procenta…

Grafický interval

• = vzdálenost mezi dvěma sousedními kótami
  • rozdíl mezi jejich číselnými hodnotami je “číselný interval“_[1]
• Poměr grafického a číselného intervalu je “modul stupnice” (M_d)_[1]
  • M_d udává, kolik jednotek jevu A se zobrazí na jednotku délky stupnice (např. na 1 mm)_[1]
    • čím větší M_d, tím větší přesnost stupnice
  • modul se odvozuje z délky L a hodnot v extrémech a_min, a a_max souboru A podle vztahu:_[1]
    • M_d = (a_max – a_min) : L
      • modul stupnice = rozdíl extrémů souboru děleno délkou stupnice mezi nimi

Síť grafu

• = soustava čar ke kvantitativní vyjádření libovolného bodu vzhledem k souřadným osám_[1]
  • pravoúhlá soustava – rovnoběžky z každého vyznačených bodů stupnic
  • polární soustava – radiální síť ze soustředných kružnic a polopřímek vycházejících z počátku pod konstantním úhlem
• Slouží pro snadnější umístění jednotlivých bodů grafu a snadnějšímu čtení_[1]
• Nesmí narušit grafický obraz
  • čáry se dělají pětkrát tenčí než čáry stupnic a znázorňovaného jevu_[1]
  • každá pátá nebo desátá čára bývá dvakrát silnější_[1]
• Jsou-li v grafu důležité jednotlivé hodnoty, může být síť hustá_[1]
• Má-li být soustředěna pozornost na graf jako celek, kreslí se síť řídká_[1]
• U popularizačních grafů síť nebývá_[1]

Klíč grafu

• = seznam použitých grafických prvků s výkladem jejich významu_[1]
  • obdoba legendy
• Umístění může být různé, dle velikosti klíče a zaplněnosti grafu_[2]
  • upřednostňuje se uvnitř v pravé dolní části pole_[2]

Vlastní grafické vyjádření vztahu

• = přímka, křivky, soustavy sloupců, soustavy bodů nebo kombinace těchto vyjádření_[2]
  • slouží pro co nejrychlejší přečtení závislosti vztahů

Vysvětlivky grafu

• Slouží k objasnění jednotlivostí v grafu_[1]
  • např. extrémů, abnormalit
• Umisťují se do pole grafu k daném prvku nebo stranou s upozorňující šipkou_[1]

Poznámky v grafu

• Určeny k objasnění detailů nutných pro správné pochopení grafu_[1]
  • mohou se týkat definic znázorňovaných ukazatelů, vysvětlovat způsob získávání dat, kvalitu dat a jejich prameny_[1]
• Umístění_[1]
  • Obecné poznámky týkající se celého grafu
    • pod název grafu nebo pod grafický obraz s odkazujícím znakem, který je i u části znaku ke které se poznámky týkají_[1]
    • delší poznámky pod pole grafu nebo výjimečně mimo graf_[2]
  • Zvláštní poznámky
    • pod pole grafu, k identifikaci se používají tzv. odkazovací znaky_[1]

Pole grafu

• = plocha, do které se umisťuje název, vlastní grafické vyjádření, stupnice, síť, klíč, vysvětlivky a poznámky_[2]
• Rozmístění prvků respektuje zásady kompozice podobné kompozici tematické mapy_[2]
  • pole grafu je obvykle uzavíráno rámem, tedy čárou vymezující graf vůči okolí_[2]

---

–> Zpět na rozcestník kartografie

Zdroje

[1] Kaňok, Voženílek: Seriál Chyby v mapách. 10 – Grafy a diagramy. Geobusiness 1/2007 – 12/2008
[2] Voženílek, V., Kaňok, J., a kol.(2011): Metody tematické kartografie – Vizualizace prostorových jevů. Grafy. Univerzita Palackého v Olomouci, 216s. 9788024427904