- Grafy lze klasifikovat podle různých hledisek:
- dle souřadných soustav
- dle počtu znázorněných proměnných
- Podle grafického znázornění dále spadají grafy do tří skupin[2]
- liniové
- sloupcové
- bodové
- Dále se grafy dělí dle počtu znázorňovaných funkcí
- jednoduché grafy
- jedna funkce znázorněná přímkou nebo křivkou, pro diskrétní jevy pak sloupce nebo body[2]
- složené grafy
- dvě a více funkcí pomocí dvou nebo více přímek či křivek[2]
- modifikace grafů
- grafy zařaditelné mezi jednoduché a složené grafy, mají ovšem zavedené názvy v odborných komunitách[2]
- Lorenzova křivka, věková pyramida – demografie
- bilanční graf – hydrologie
- větrná růžice – klimatologie
- histogram – statistika
- grafy zařaditelné mezi jednoduché a složené grafy, mají ovšem zavedené názvy v odborných komunitách[2]
- jednoduché grafy
1. Dle počtu proměnných
Závislost dvou proměnných
- Dělí se na jednoduché a složené grafy
Jednoduché grafy
- Znázornění vztahu dvou proměnných pomocí jedné funkce
- graf obsahuje jednu přímku nebo křivku[2]
- diskrétní jevy zpravidla pomocí sloupců či bodů
- spojité jevy zpravidla křivka
- graf obsahuje jednu přímku nebo křivku[2]
- Používá se pravoúhlá nebo polární (kruhová) soustava
- osa x obvykle pro hodnoty nezávislé proměnné
- osa y obvykle pro hodnoty závislé proměnné
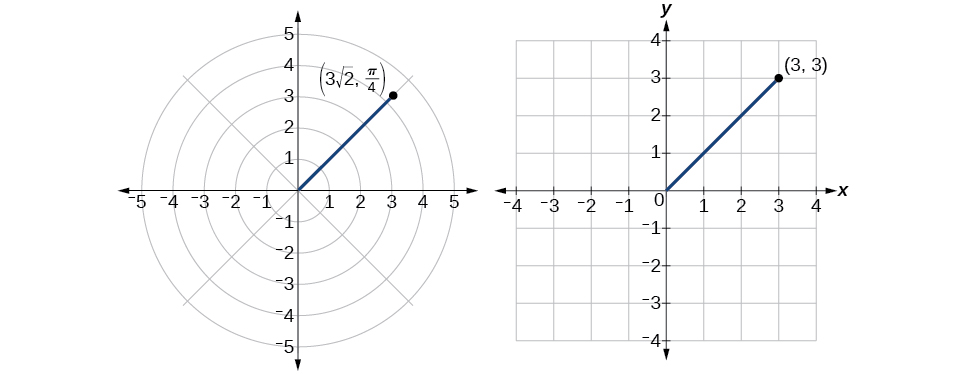
- Pro lepší čitelnost a přehlednost se obvykle plocha grafu mezi výslednou křivkou a osou x vyplňuje nevýraznou barevnou plochou[2]
Složené grafy
- Znázornění dvou a více funkcí za pomoci dvou a více křivek
- ve zvláštních případech lze pro diskrétní jevy použít soustavu sloupců nebo bodů[2]
- Pro pravoúhlou soustavu obvykle platí[2]:
- osa x užívána pro hodnoty nezávislé proměnné
- osa y užívána pro hodnoty závislé proměnné
Pravoúhlé liniové grafy
Jednoduché pravoúhlé liniové grafy
- Vhodné pro funkční závislosti[1]
- vznikají spojením bodů závislé proměnné
- Průběh linie je závislý na měřítku grafu a zvolené stupnici[1]
- stupnice mohou být na obou osách stejné, nebo různé
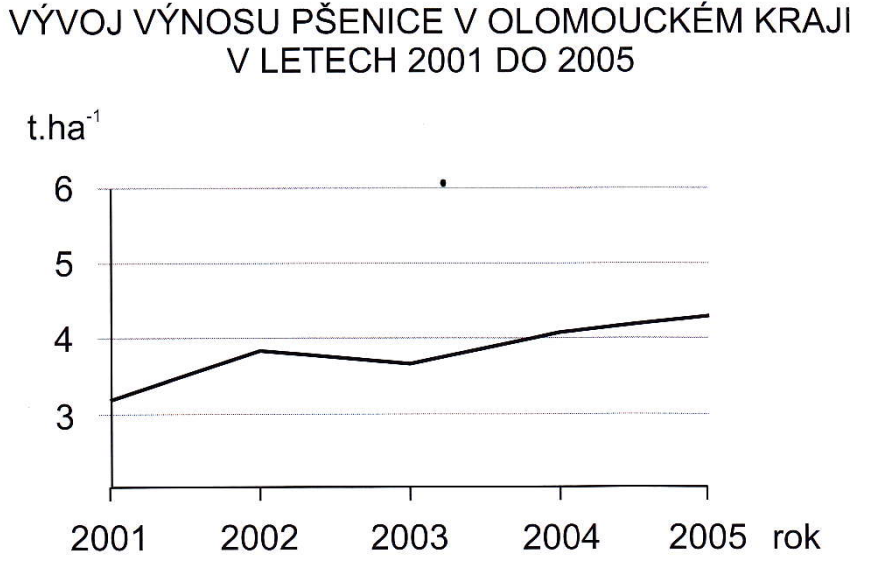
- Používané stupnice:
- aritmetická
- = osy rozděleny na stejné dílky[1]
- ukazuje absolutní změny[1]
- logaritmická
- = kombinace dvou logaritmických stupnic[2]
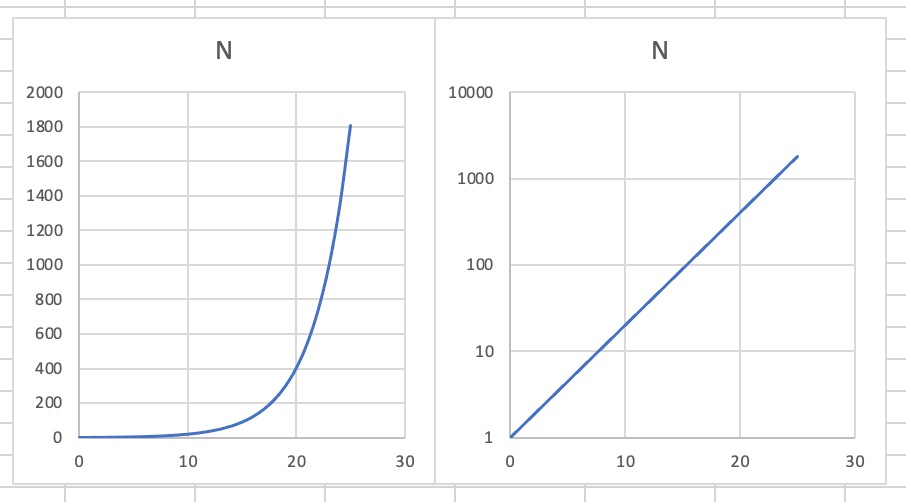
- semilogaritmická
- = použití logaritmické stupnice na jedné ose a logaritmické na druhé ose[1]
- mění exponenciálu na přímku[1]
- ukazuje tempo změn[1]
- variační
- = kombinace aritmetické a pravděpodobnostní stupnice[2]
- aritmetická
Zdroj
- Pro zvýraznění změn možné jednotkové úsečky na jedné ose zmenšit a na druhé zvětšit[2]
- může ale dojít k mystifikaci čtenáře, viz obrázek[2]
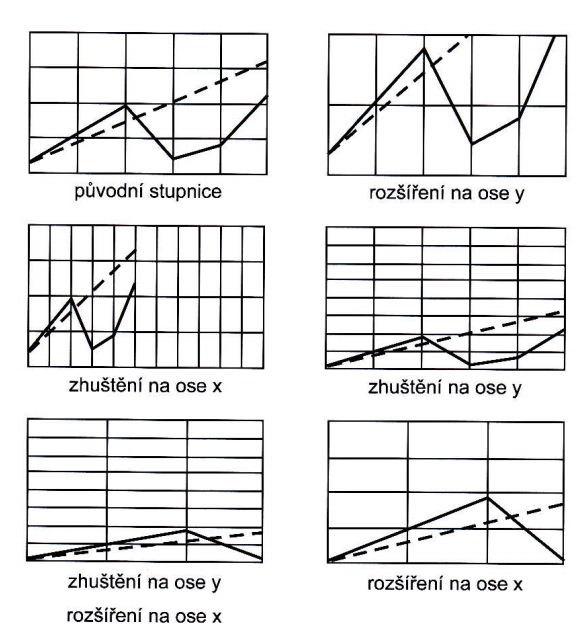
Zdroj [2]
Složené pravoúhlé liniové grafy
- Vyjadřují vztahy mezi více soubory vyjádřené několika liniemi[2]
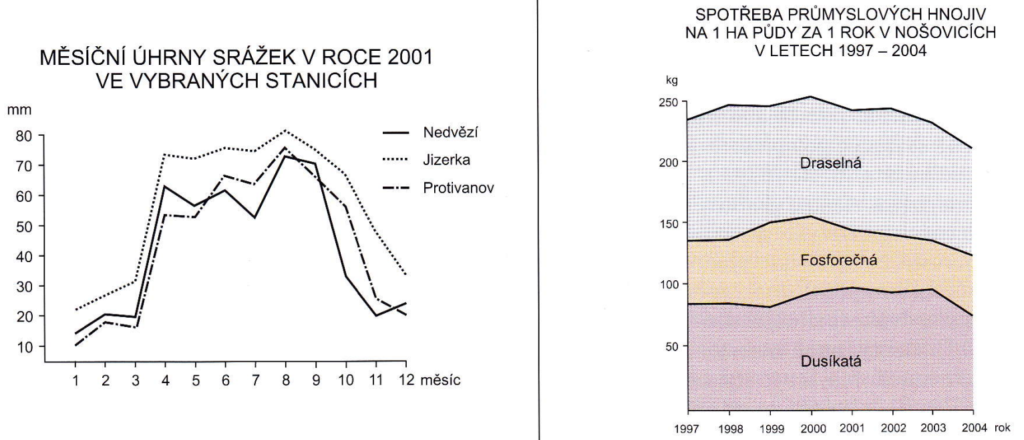
vlevo ekvivalentní (rovnocenný) – vpravo sumační (součtový)
Zdroj [2]
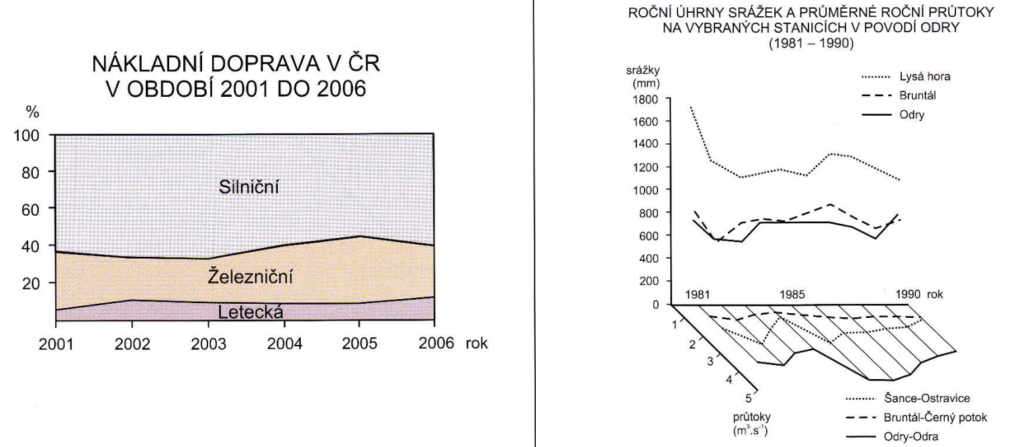
vlevo strukturní – vpravo vztahový (rovnocenný)
Zdroj [2]
Modifikace pravoúhlých liniových grafů

vlevo frekvenční graf (graf četnosti) – vpravo graf střední hladiny (indexové hladiny)
Zdroj [2]
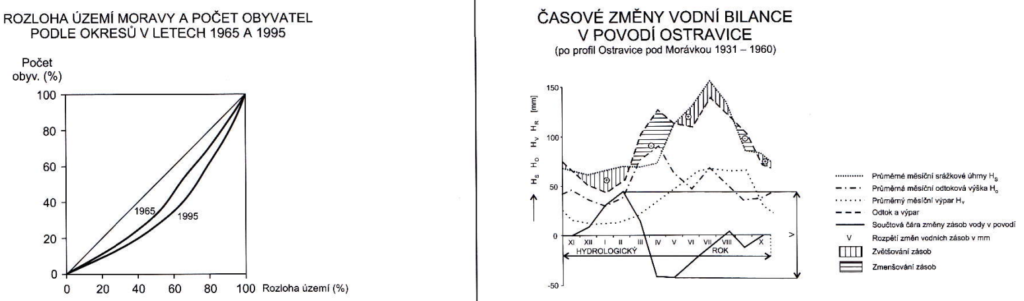
vlevo Lorenzova křivka (koncentrační křivka) – vpravo bilanční graf
Zdroj [2]

vlevo vícestupnicový graf – vpravo amplitudový graf
Zdroj [2]
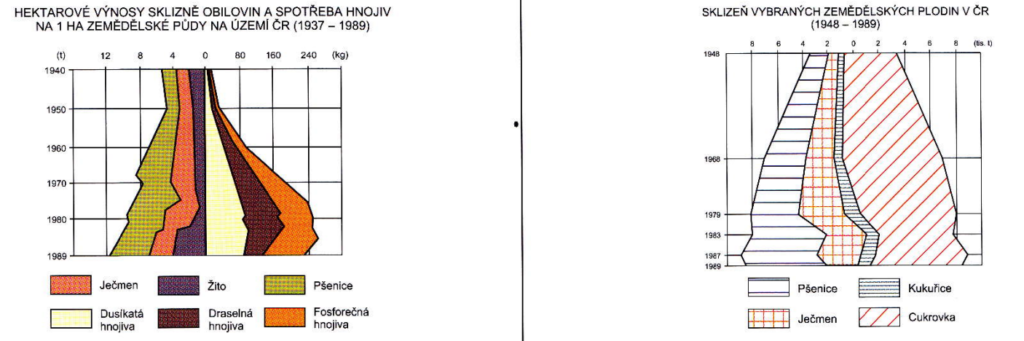
vlevo proudový součtový, symetrický – vpravo proudový součtový, osový
Zdroj [2]
Pravoúhlé sloupcové grafy
Jednoduché pravoúhlé sloupcové grafy
- Zobrazují jevy nespojitě (diskrétně)
- použití k vyjádření rozdílů v nespojité řadě a ke znázornění krátkých řad[1]
- často ve spojení s liniovým grafem – k vyjádření rozdílů mezi spojitými a nespojitými daty[2]
- Hojné použití na tematických mapách[1]
- rozdíl čtyř jevů vyjádřen čtyřmi sloupci
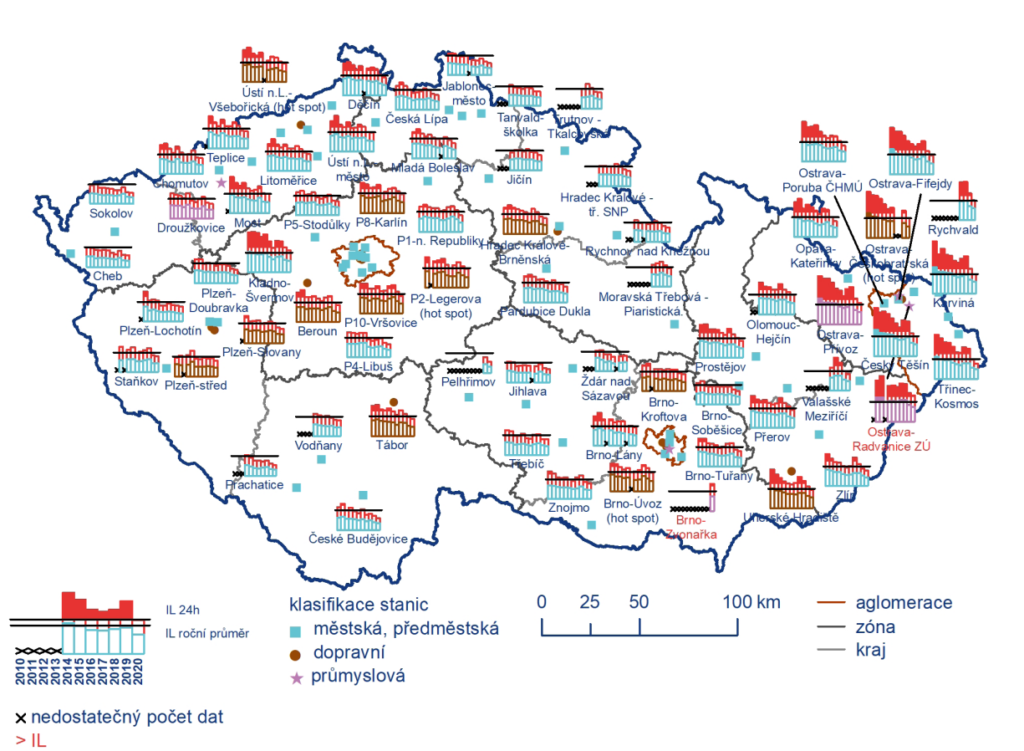
- Nevhodné pro srovnání více jak dvou časových řad nebo příliš dlouhých časových řad[1]
- Konstrukce grafu:[1]
- tvar sloupců – nemá zásadní význam, mohou být nahrazeny obrazcem, symbolem, zvýrazněny…
- výška sloupce – zásadní, rozhoduje o velikosti jevu
- šířka sloupce – musí být konstantní, nenese žádnou statistickou hodnotu
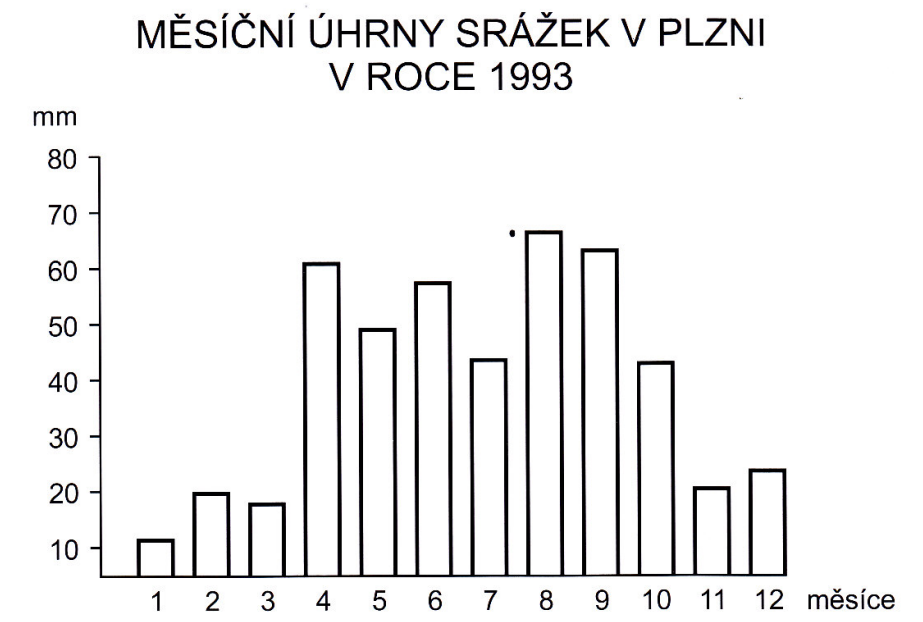
- Hodnoty závislé proměnné jsou v grafu tvořeny sloupci kolmými k ose x
- sloupce mohou být dle potřeby umístěny i na osu y, tedy vodorovně
Složené pravoúhlé sloupcové grafy
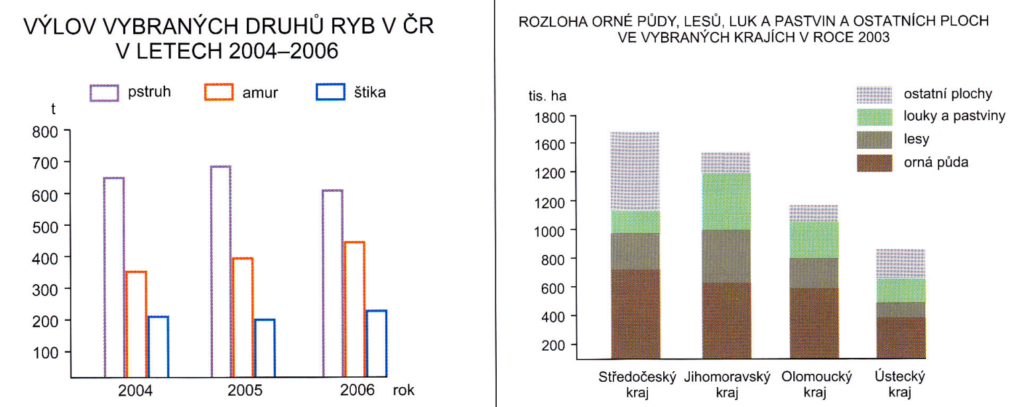
vlevo skupinový – vpravo sumační (součtový)
Zdroj [2]
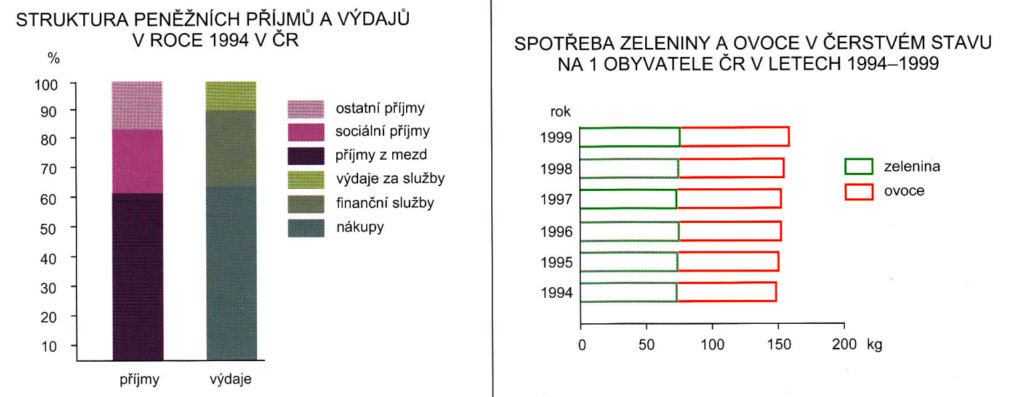
vlevo strukturní – vpravo vodorovný sumační
Zdroj [2]
Modifikace pravoúhlých sloupcových grafů
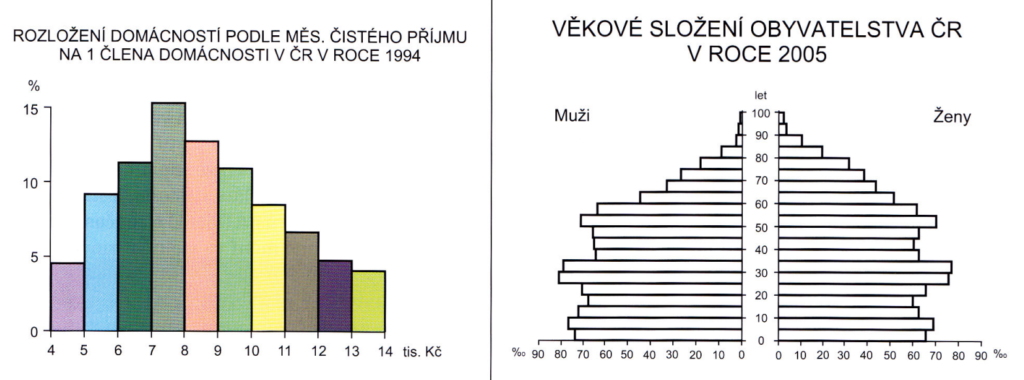
vlevo histogram (graf četností) – vpravo histogram párový
Zdroj [2]
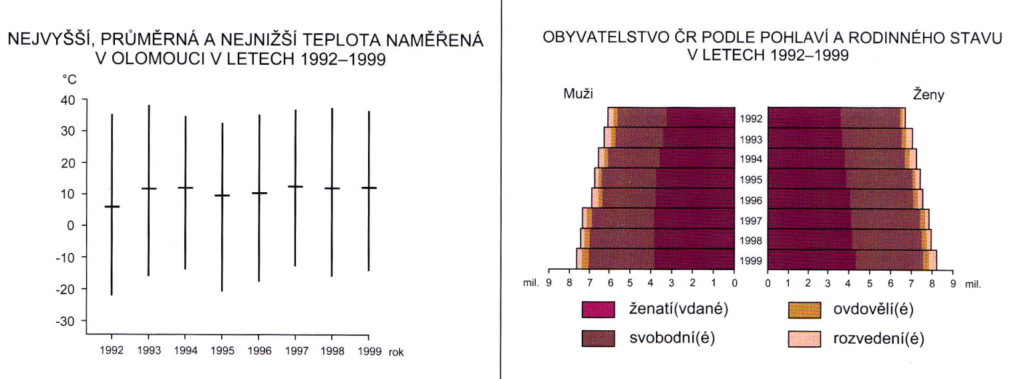
vlevo amplitudové sloupce – vpravo sloupce párové součtové
Zdroj [2]

vlevo strukturálně dělené sloupce (osové) – vpravo obrázkové sloupce
Zdroj [2]
Pravoúhlé bodové grafy
- Ke znázornění koncentrace nebo rozložení skupiny jevů[1]
- každý bod v grafu je znázorněním závislosti dvou proměnných
- skupina bodů znázorňuje korelaci dvou proměnných
- kladná korelace – stoupající přímka
- záporná korelace – klesající přímka
- osa x a y musí mít stejnou délku
- = poje grafu je čtvercové
- Nejsou určeny do použití v mapě[1]
- Časté použití časového úseku (rok, měsíc..) místo druhé proměnné[2]
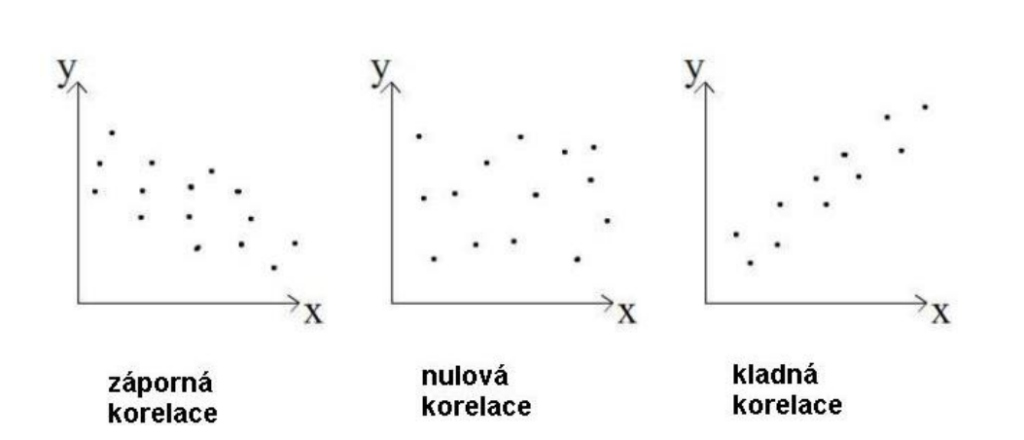
Kruhové grafy
- = sít radiálních polopřímek a soustředných kružnic
- jedna polopřímka (zpravidla vertikální směrem nahoru) je základní, k ní se dále ve směru hodinových ručiček nanáší další přímky o stanovený úhel[1]
- polopřímky nejčastěji znázorňují průběh času[1]
- dělení 360° takřka neomezené
- nejčastěji na 7 dílů (dny v týdnu), 8 dílů (hodiny ve směně), 12 dílů (měsíce) nebo 24 dílů (hodiny za den)
Kruhové liniové grafy
- Pro cyklicky se opakující jevy
- na základní polopřímce se potkává první a poslední hodnota jevu[2]
- kruhová síť opticky vytváří představu nepřetržitého vývoje daného jevu[1]
- automaticky se řadí odpovídající hodnoty příslušného cyklu vedle sebe[2]
- Dvě řady hodnot s rovnoběžnými úsečkami = stejná sezónnost nebo stejné tempo růstu[2]

Jednoduché kruhové liniové grafy

vlevo otevřený – vpravo uzavřený
Zdroj [2]
Složené kruhové liniové grafy

vlevo ekvivalentní (rovnocenný) otevřený – vpravo ekvivalentní (rovnocenný) uzavřený
Zdroj [2]

vlevo sumační (součtový) – vpravo strukturní
Zdroj [2]
Modifikace kruhových liniových grafů

vlevo graf střední hladiny (indexové hladiny) – vpravo amplitudový graf
Zdroj [2]
Kruhové sloupcové grafy
- Obdoba sloupcových grafů
- Dvojího typu:[2]
- 1. použité sloupců stejné šířky
- sloupce vybíhají jako paprsky z počátečních souřadnic (pólu)
- délka sloupce vyjadřuje hodnotu jevu
- aby nedocházelo v pólu ke slévání počátků sloupců, jsou počátky posunuty o určitou vzdálenost, čímž vznikne okolo pólu prázdný kruh
- 2. použití kruhových výsečí
- plocha výseče vyjadřuje hodnoty znázorňovaného jevu
- délka není vhodná, plocha narůstá mnohem více, viz orázek
- plocha výseče vyjadřuje hodnoty znázorňovaného jevu
- 1. použité sloupců stejné šířky
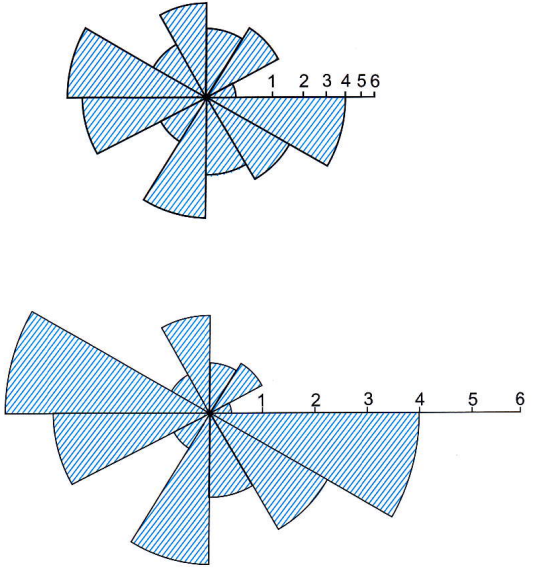
nahoře – stupnice vytvořena na základě plochy
dole – stupnice vytvořena na základě délky
Jednoduché kruhové sloupcové grafy
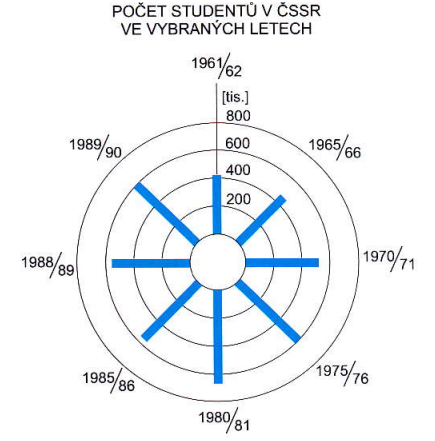
Zdroj [2]
Složené kruhové sloupcové grafy
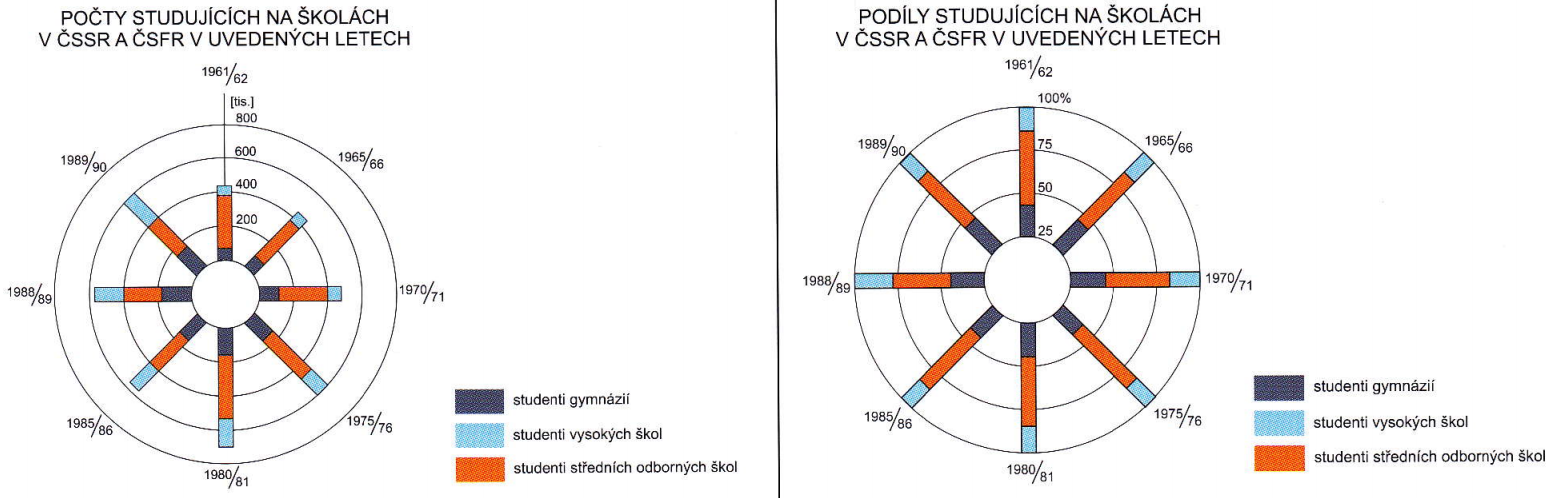
vlevo sumační (součtový) – vpravo strukturní
Zdroj [2]
Modifikace kruhových sloupcových grafů
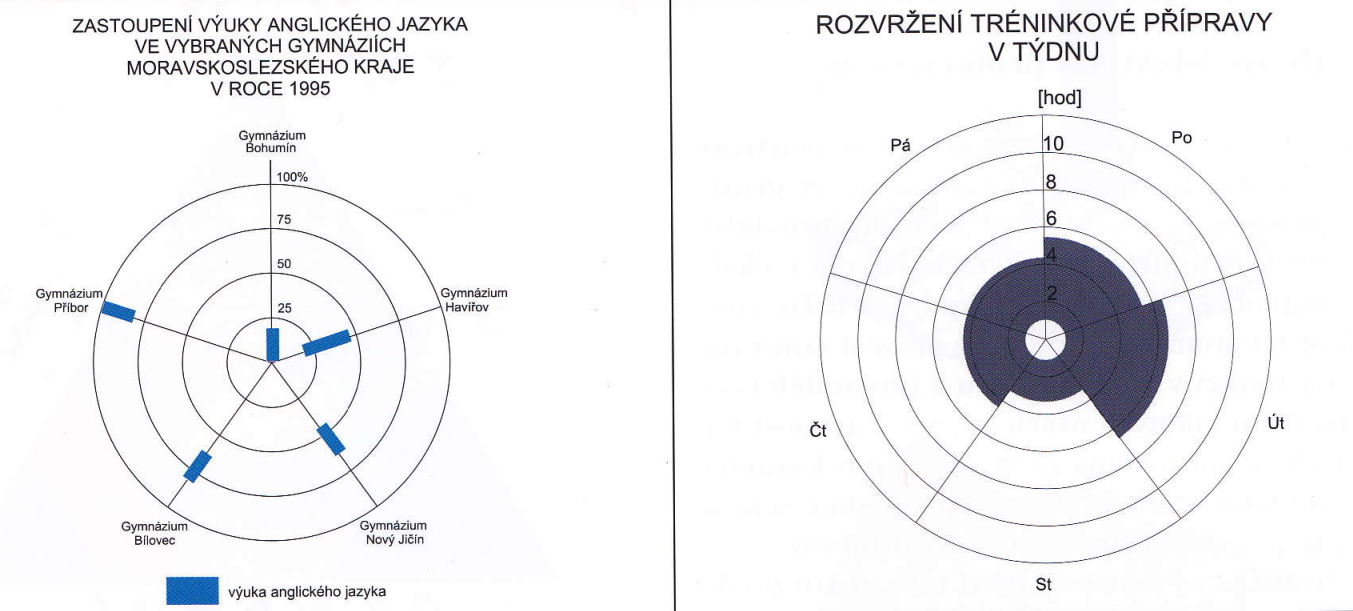
vlevo pohyblivé sloupce – vpravo výsečový jednoduchý
Zdroj [2]
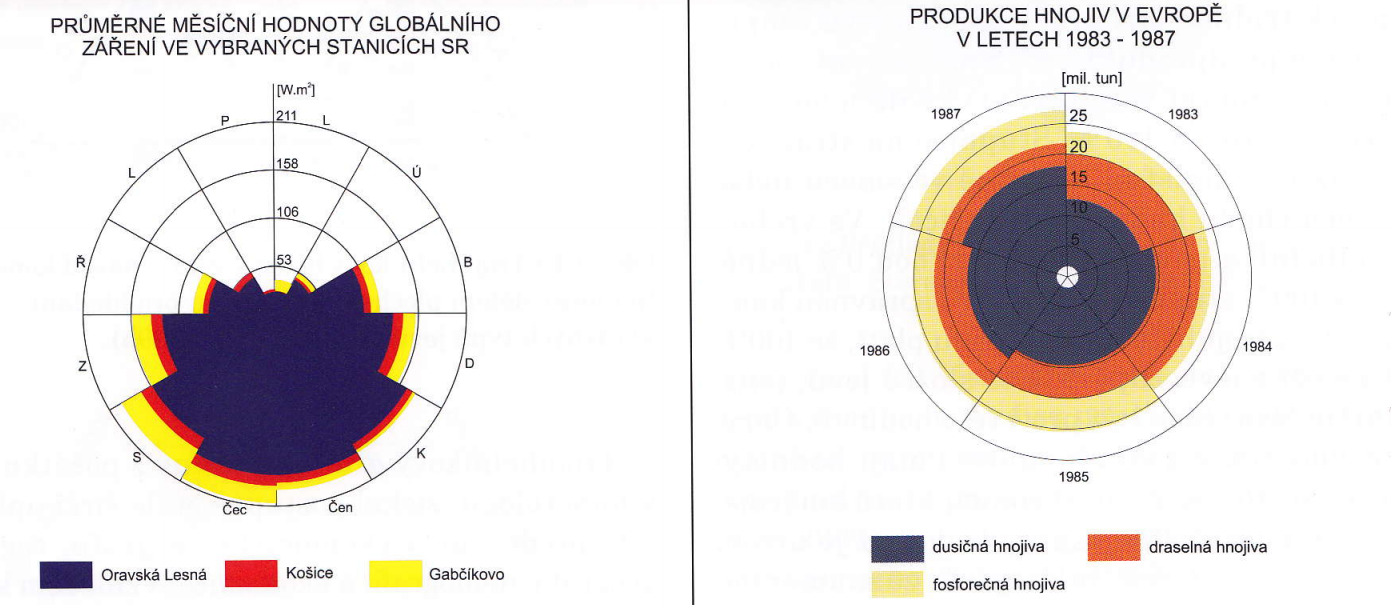
vlevo výsečový složený, srovnávací – vpravo výsečový složený součtový
Zdroj [2]
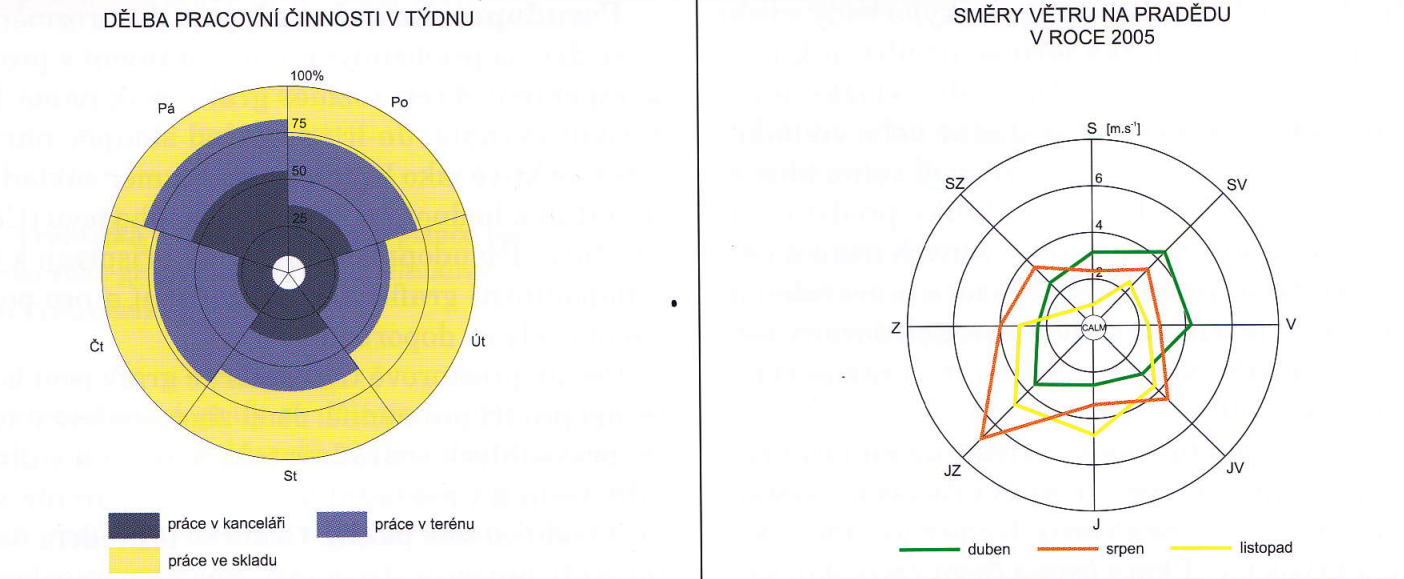
vlevo výsečový složený strukturní – vpravo větrná růžice
Zdroj [2]
Závislost tří proměnných
- Používají se grafy se třemi souřadnicemi
- grafy trojúhelníkové a pseudoprostorové
Trojúhelníkové grafy
- = rovnostranný trojúhelník, kde každá strana je jednou osou souřadnic[1]
- Součet všech tří prvků daného jevu je 100 %[1]
- každá osa je část třídílné struktury[1]
- např. obyvatelstvo předproduktivní, produktivní a postproduktivní[1]
- stupnice na grafu ve směru nebo proti směru hodinových ručiček
- ve vrcholu trojúhelníka současně leží bod 0 % jedné stupnice a zároveň 100 % druhé stupnice[1]
- každá osa je část třídílné struktury[1]

- Větší koncentrace bodů u některého z vrcholů svědčí o nevyrovnanosti podílu složek ve sledovaném jevu[1]
- trojúhelníkový graf je obměnou grafu koncentrace bodů[2]
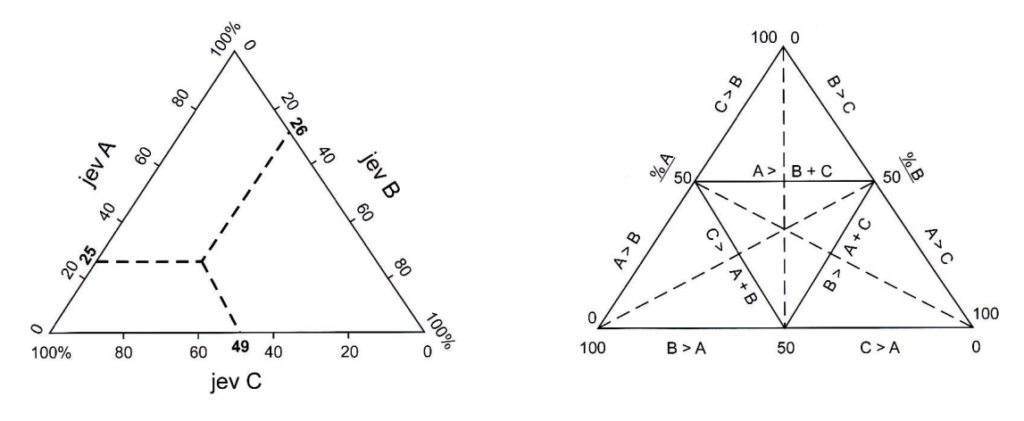
Zdroj [2]
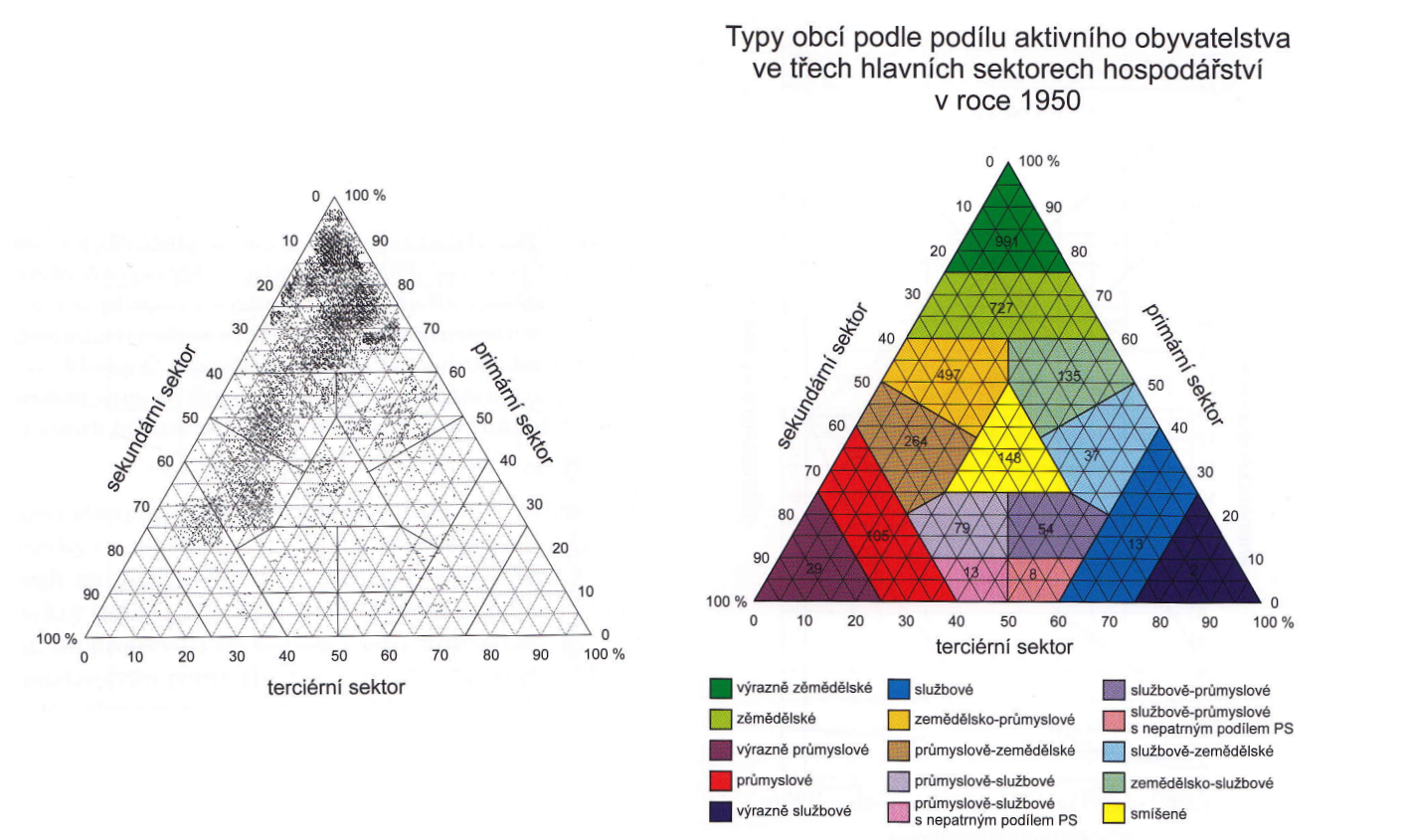
- Trojúhelníkovým grafem lze srovnat i časový vývoj struktury znázorňovaného jevu
- tzv. trojúhelníkový liniový graf
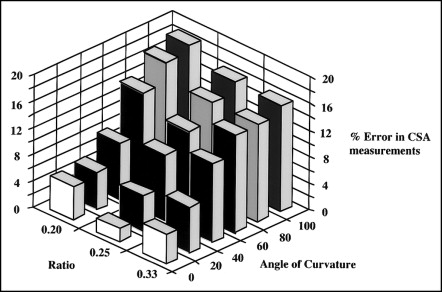
Pseudoprostorové grafy
- Zhotovovány v systému tří pravoúhlých souřadnic[1]
- osy x a y tvoří základní plochu, osa z je vzdálenost od této plochy
- Jejich používání se obecně nedoporučuje
- na pohled působí zajímavě, snadno se ovšem znepřehlední a odečítání údajů může čtenáři působit obtíže
- vhodné použití pouze pokud se nepožaduje odečítání přesných hodnot, ale jen srovnání a vytvoření představ o rozložení jevu[2]
2. Dle souřadných soustav
1. Grafy pravoúhlé
- Zobrazení v pravoúhlé souřadné soustavě[2]
- = dvě navzájem kolmé osy (rovina)
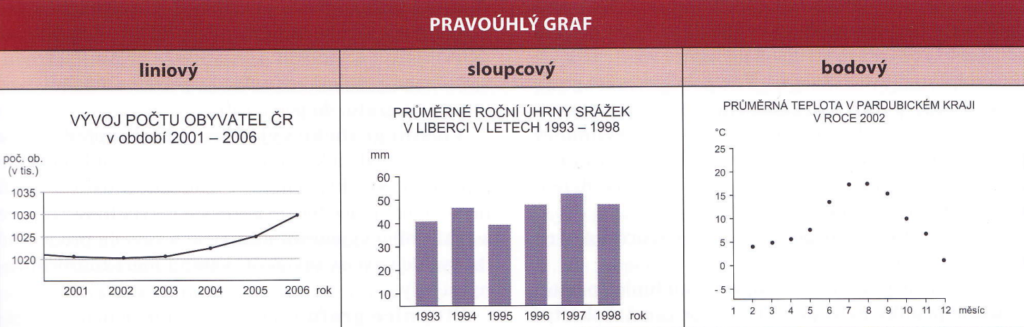
2. Grafy kruhové
- Zobrazení v polární soustavě[2]
- = soustava trsu polopřímek a soustředných kružnic v rovině
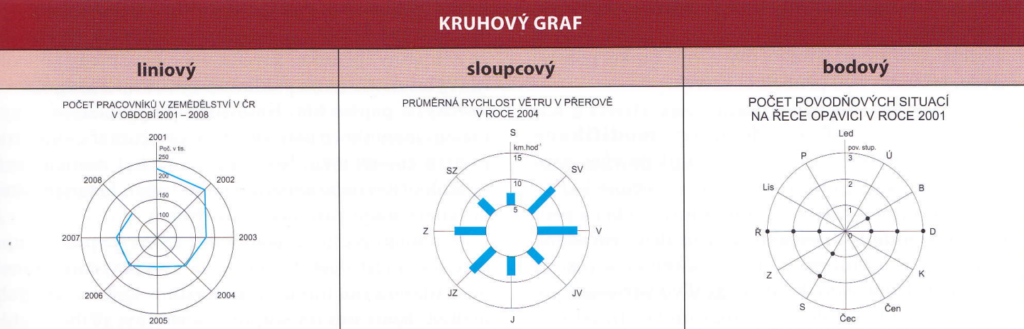
3. Grafy trojúhelníkové
- Zobrazení za pomocí tří stran rovnoramenného trojúhelníku jako tří os v rovině[2]

4. Grafy pseudoprostorové
- Zobrazení v soustavě tří kartézských os v pseudoprostoru[2]
- = tři osy uspořádané tak, aby vytvářely dojem trojrozměrného prostoru

–> Zpět na rozcestník kartografie
Zdroje
[1] Kaňok, Voženílek: Seriál Chyby v mapách. 10 – Grafy a diagramy. Geobusiness 1/2007 – 12/2008
[2] Voženílek, V., Kaňok, J., a kol.(2011): Metody tematické kartografie – Vizualizace prostorových jevů. Grafy. Univerzita Palackého v Olomouci, 216s. 9788024427904