- Určuje se šířka a hranice intervalů[1]
- předkládá pouze meze hodnot hranice intervalu, ve kterém se hodnota nachází[1]
- Není možní zjistit konkrétní hodnotu[1]
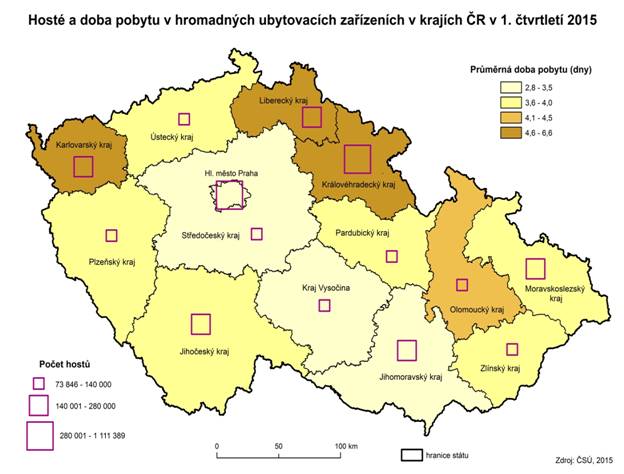
- Přesné pravidlo pro určení počtu intervalů neexistuje, pouze pomocná doporučení (viz vzorec)[1]
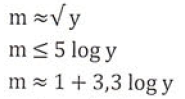
y = počet statistických jednotek v souboru
Zdroj [1]
- Nejčastěji je doporučováno 4 až 10 intervalů, v závislosti na druhu použité metody[1]
- počet intervalů je omezen schopností oka rozeznávat odstíny barvy či jemnost rastru
- ovlivněno taktéž účelem mapy
- mnoho intervalů = příliš rozdrobená mapa[3]
- málo intervalů = pouze hrubá informace[3]
- Hodnoty z intervalů stupnice musí mít své grafické vyjádření v mapě[1][2]
- interval nesmí obsahovat pouze jednu hodnotu[1]
- intervalová stupnice proto není vhodná pro znázorňování málo početných souborů[1]
- Účelem intervalové stupnice je regionalizovat jev[1]
- Pro kartodiagramy (s intervalovou stupnicí) se parametry diagramů počítají ze středu intervalu[1]
- parametry – např. strany čtverců, trojúhelníků…
Druhy intervalových stupnic
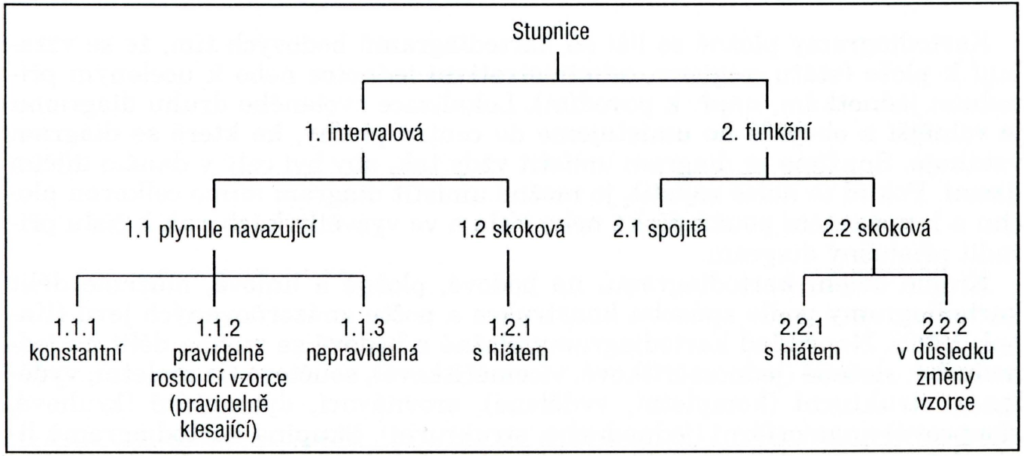
Dělení stupnic dle [2], každá stupnice je určena pro dané rozdělení statistického souboru. Názorná ukázka použití dané stupnice na datech je v kapitole “Obecný postup tvorby intervalové stupnice”. Kapitola s rozdělením stupnic je pak návodem pro ostatní rozdělení, jenž nejsou v obecném postupu.
1.1. Stupnice intervalové – plynule navazující
- Intervaly na sebe plynule navazují
- Nejpropracovanější a nejpoužívanější stupnice[2]
- Stupnice odvozené od mediánu nebo průměru (ve skupině nepravidelných) je třeba zvážit s přihlédnutím k účelu mapy[2]
- největší pravděpodobnost výskytu v Gaussově rozdělení je v oblasti průměru, proto při vložení hranice intervalu do průměru dojde k symetrickému rozdělení homogenních hodnot[2]
- oblast homogenity bude rozdělena ve dvou intervalech na nadprůměrné a podprůměrné hodnoty
- autor se musí rozhodnout, zdali nechce ukázat oblast homogenity jako samostatný interval
- největší pravděpodobnost výskytu v Gaussově rozdělení je v oblasti průměru, proto při vložení hranice intervalu do průměru dojde k symetrickému rozdělení homogenních hodnot[2]

Zdroj [1]
1.1.1. Konstantní stupnice
- 1.1.1.1. Stupnice s rovnoměrným rozdělením celé šíře souboru intervaly o konstantní délce[2]
- používá se především při prvotním přiblížení datového souboru pro tvorbu histogramu četností[2]
1.1.2. Pravidelně rostoucí (klesající) stupnice
- 1.1.2.1. Pravidelná geometrická stupnice
- běžně se nepoužívá[2]
- vyznačuje se pravidelně rostoucími intervaly – každý další interval je dvakrát širší, než předchozí[2]
- např. 5,1 – 10,0; 10,1 – 20,0; 20,1 – 40,0; 40,1 – 80,1…
- 1.1.2.2.Logaritmická stupnice
- běžně se nepoužívá[2]
- 1.1.2.3. Všechny další stupnice s matematicky definovanou posloupností
- ale pouze pokud se velikost následujícího intervalu zvětšuje (zmenšuje)[2]
- použití jen v teoretickém výzkumu[2]
- ale pouze pokud se velikost následujícího intervalu zvětšuje (zmenšuje)[2]
1.1.3. Nepravidelné stupnice
- 1.1.3.1.Stupnice s rovnoměrným rozdělením úseku velkých četností jevu, ve kterých je oblast minimálních výskytů omezena do jednoho až dvou intervalů
- u normálního rozdělení[2]
- u extrémně levostranného nebo pravostranného rozdělení četností[2]
- u rozdělení blízkého exponenciálnímu[2]
- u rozdělení typu U[2]
- u rozdělení Pearsonovy křivky třetího typu[2]
- 1.1.3.2.Stupnice s exponenciálním rozdělením variační šíře úseku velkých četností
- úsek velkých četností je rozdělen exponenciálně a oblast minimálních výskytů do jednoho až dvou intervalů[2]
- 1.1.3.3.Stupnice sedlové
- u vícevrcholového rozdělení četností[2]
- hranice intervalů jsou definovány minimy (event. inflexními body) průběhu rozdělení četností[2]
- podobně definované hranice jsou i u jednovrcholového rozdělení četností (Gaussovo normální rozdělení)[2]
- 1.1.3.4.Stupnice odvozené od průměru celého souboru
- u normálního rozdělení souboru[2]
- a) průměr xprům a směrodatná odchylka s
- hranice intervalů jsou (∞; xprům – s⟩; (xprům – s; xprům⟩; (xprům; xprům + s⟩; (xprům + s; ∞⟩
- b) průměr xprům a dvojnásobek směrodatné odchylky 2s
- hranice intervalů jsou (∞; xprům – 2s⟩; (xprům – 2s; xprům⟩; (xprům; xprům + 2s⟩; (xprům + 2s; ∞⟩
- c) průměr xprům a průměrná odchylka od průměru d
- hranice intervalů jsou (∞; xprům – dx⟩; (xprům – dx; xprům⟩; (xprům; xprům + dx⟩; (xprům + dx; ∞⟩
- 1.1.3.5.Stupnice odvozené od mediánu celého souboru
- u normálního rozdělení souboru[2]
- a) medián xmed, dolní kvartil x25 a horní kvartil x75
- hranice intervalů jsou (∞; x25⟩; (x25; xmed⟩; (xmed; x75⟩; (x75; ∞⟩
- b) medián xmed a pentily nebo výjimečně decily
1.2. Stupnice intervalové – skokové
- Stupnice, ve kterých je jeden či více intervalů vypuštěno[2]
- stupnice není plynulá, vznikne mezera – hiját
- důvodem vypuštění intervalu může být pouze neexistence hodnot v mapě pro daný interval[2]
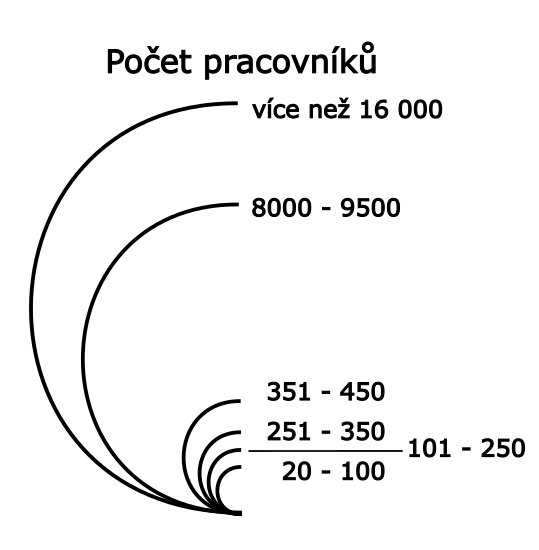
Nejnižší tři stupně na sebe navazují (druhý propojen vodící linkou), rozmezí 8000 – 9500 je oboustranně odděleno hiáty.
1.2.1. Stupnice skokové s hijátem
- 1.2.1.1. Stupnice aritmetická s hijátem
- 1.2.1.2. Stupnice geometrická s hijátem
- 1.2.1.3. Stupnice logaritmická s hijátem
- 1.2.1.4. Stupnice s matematicky definovanou posloupností s hijátem
- 1.2.1.5. Stupnice sedlová s hijátem
Obecný postup tvorby intervalové stupnice
- 1. Vytvoří se histogram četností
- tzn. rozdělení datové sady do vhodných stejných intervalů[1]
- takové intervaly, ve kterých se data rozloží tak, aby četnost jevu (n) byla rozložena v téměř celé šíři výskytu[1]
- 2. Poté se intervaly histogramu proloží křivka hodnot výskytu jevu v intervalech[1]
- některé intervaly budou mít vyšší počet výskytů než jiné
- 3. Křivka četností se následně porovná s možnými teoretickými četnostmi výskytu[1]
- viz obrázky
- 4. Provede se testování normality rozdělení (kromě vícevrcholového)[2]
- 5. Vytvoří se stupnice podle povahy rozdělení četností[2]
- 6. Zvolí se vhodné barvy nebo rastry[2]
Postup pro nejběžnější rozdělení
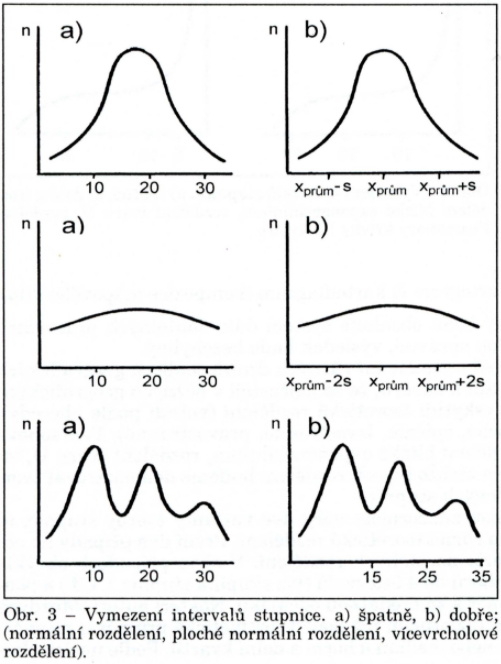
normální rozdělení, ploché normální rozdělení a vícevrcholové rozdělení
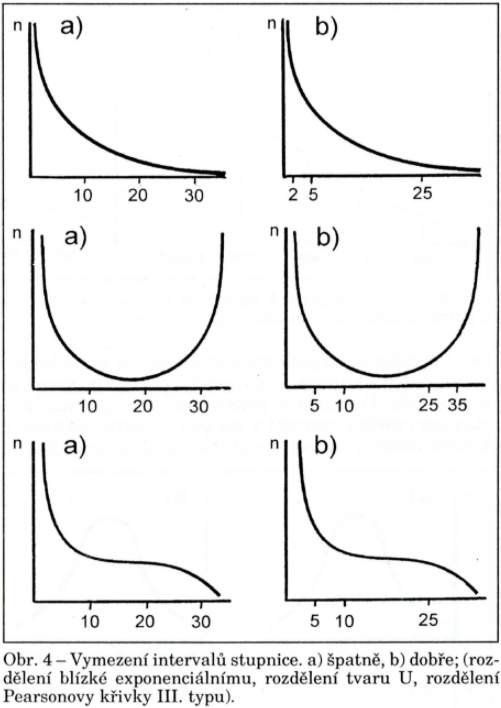
rozdělení blízké exponenciálnímu, rozdělení tvaru U, rozdělení Pearsonovy křivky III. typu
- Normální a ploché normální rozdělení četností
- používá se rozdělení souboru do 4 intervalů[1]
- vzniknou intervalové, plynule navazující stupnice o nepravidelných šířkách[1]
- krajní intervaly normálního rozdělení sahají do nekonečna, proto nemohou být intervaly rovnoměrné[1]
- k vymezení se používá aritmetický průměr (xprům) a směrodatná odchylka (s)
- pokud je norm. rozdělení ploché, lze použít k rozdělení dvojnásobek směrodatné odchylky[1]
- pokud potřebujeme více než 4 intervaly, lze použít např. decily[1]
- rozdělení na 10 intervalů ale může být problém pro interpretaci a přehlednost
- Vícevrcholové rozdělení četností
- ukazuje na nesourodý statistický soubor[1]
- každý vrchol ukazuje oblast dat s typickou společnou vlastností[1]
- intervaly vymezíme tak, že interval zahrnuje vrchol a nejbližší okolí[1]
- hraniční body obvykle v sedlech křivky[1]
- ukazuje na nesourodý statistický soubor[1]
- Rozdělení četností blízké exponenciálnímu
- v souboru je velké množství nízkých hodnot[1]
- rozděluje se na úsek četných nízkých hodnot do několika exponenciálně dělených intervalů a úsek minimálních výskytů v jednom až dvou intervalech[3]
- Rozdělení typu U a rozdělení Pearsonovy křivky III. typu
- v geografických disciplínách méně častý výskyt
- řazení do pravidelných intervalů oblasti nejvyšších a nejnižších výskytů jevu, oblast (relativně) rovnoběžná s osou x je v jednom širším intervalu[1]
- snaha zachytit něco společného do jednoho intervalu[1]
–> Zpět na rozcestník kartografie
Zdroje
[1] Kaňok, Voženílek: Seriál Chyby v mapách. 8 – Stupnice. Geobusiness 1/2007 – 12/2008
[2] Kaňok: Kartogram a kartodiagram – stanovení objektivní stupnice. Sborník české geografické společnosti. Rok 1999, číslo 4, ročník 106.
[3] Voženílek, V., Kaňok, J., a kol.(2011): Metody tematické kartografie – Vizualizace prostorových jevů. Stupnice v kartografii. Univerzita Palackého v Olomouci, 216s. 9788024427904
